Výpočet vzdálenosti Země - Slunce pozorováním přechodu Venuše před Sluncem

Výpočet vzdálenosti Země – Slunce pozorováním přechodu Venuše před Sluncem

Zde si můžete stáhnout tento dokument v PDF [205kB].

Úkol:

Změřit vzdálenost Země–Slunce (tzv. astronomickou jednotku – AU) pozorováním přechodu Venuše ze dvou míst na Zemi ležících na stejném poledníku. AU je možno určit také pozorováním z míst s různou zeměpisnou délkou, ale matematický výpočet je mnohem složitější. Zde uvedeme zjednodušenou metodu, která byla použita při prvním pozorování v 18. století.

Předpoklady:

Chceme-li nabídnout metodu přístupnou středoškolským studentům, musíme učinit tyto zjednodušující předpoklady:

dvě pozorovací stanoviště, jejich průměty na slunečním povrchu a středy Země, Slunce a Venuše leží v téže rovině
dráhy Venuše a Země při oběhu kolem Slunce jsou kruhové.

Základní znalosti potřebné k řešení:

Na základě předešlých předpokladů potřebují studenti znát pouze:

Matematické znalosti
1. Součet tří úhlů v trojúhelníku je 180 stupňů.
2. Přímou úměru nebo Pythagorovu větu
3. Definici funkce sinus
Astronomické znalosti
1. Třetí Keplerův zákon
2. Definici horizontální paralaxy

Úvod:

Za účelem pozorování přechodu Venuše v letech 1761 a 1769 vynaložil Sir Edmund Halley velké úsilí a Jean-Nicolas Delisle shromáždil všechna pozorovaná data. Použijeme jejich pozorování k výpočtu vzdálenosti Země-Slunce pomocí zjednodušené metody s pozorovateli na tomtéž poledníku. Pozorovatelé byli rozmístěni v zeměpisných šířkách co nejdále od sebe z důvodu dosažení co největší přesnosti měření.

Vybraná místa byla často velmi daleká a dostat se na ně bylo tehdy velmi nebezpečné z důvodů bouří a válek mezi národy. Zvláště nebezpečná byla oblast Indického oceánu kvůli válce mezi Anglií a Francií. Musíme zdůraznit, že přechod Venuše v roce 1761 byl prvním, pro který bylo zorganizováno asi 130 mezinárodních expedic pokrývajících celý svět. V roce 1769 se uskutečnily expedice do míst Pondichery (Madras), Saint Domingo (Západní Indie), San José del Cabo (Baja California), Hudsonův záliv (Canada), Papeete (Tahiti), Vardö (Laponsko), Cajanebourg (poloostrov Kola) a Jakutsk (Sibiř). Celkem se jich zúčastnilo 151 pozorovatelů na 77 různých místech. Expedice měly různé obtížné úkoly, některé velmi vzrušující, a ne vždy výsledky splnily očekávání!

Pozorování ze Země:

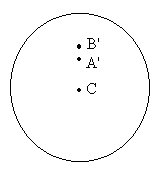
Předpokládejme, že dva pozorovatelé jsou na dvou různých místech Země A a B na stejném poledníku (mají stejnou zeměpisnou délku), ale značně odlišnou zeměpisnou šířku. Venuše se promítá pozorovatelům jako malý disk na slunečním kotouči ve dvou různých místech A' a B'. To je dáno tím, že pozorovací přímky z bodů A a B směrem k Venuši jsou různé.

S pomocí referenčních hvězd umístíme oba obrázky tak, aby se překrývaly, čož nám umožní změřit obloukovou vzdálenost (paralaxu). Překryjeme-li oba obrázky s totožnými středy Slunce C, je pak oblouková vzdálenost A' a B' stejná jako oblouková vzdálenost dvou pozic Venuše pozorovaných z míst A a B.

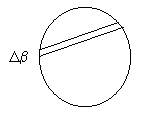
Budeme-li pozorovat pohyb Venuše během celého přechodu, můžeme zakreslit pozice středu Venuše během pozorování. Při pozorování ze dvou míst A a B dostaneme dvě rovnoběžné úsečky, odpovídající vždy jednomu z těchto míst. Úhlovou vzdálenost úseček označme δβ.

Jak změřit vzdálenost Země - Slunce

Uvažujme rovinu definovanou třemi body: střed Země O, střed Slunce C a střed Venuše V. Pokud jsou dva pozorovatelé na stejném poledníku v místech A a B, jejich průměty Venuše na slunečním disku jsou body A' a B'.

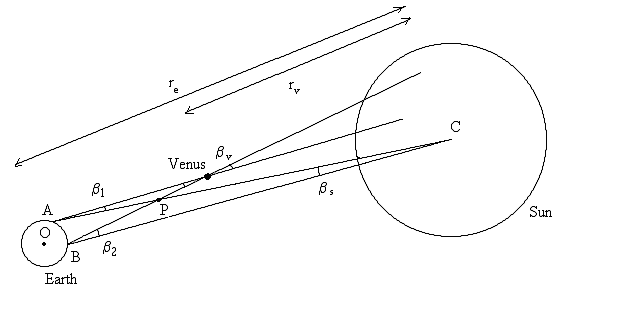
Trojúhelníky APV a BPC mají stejné vnější úhly při vrcholu P a tak součty jejích úhlů při zbylých dvou vrcholech jsou stejné,

β_v + β₁ = β_s + β₂

z toho

β_v - β_s = β₂ - β₁ = Δβ

Zde Δβ je úhlová vzdálenost dvou různých stop Venuše na slunečním disku měřených dvěma pozorovateli. Úpravou poslední rovnice dostaneme

Δβ= β_s ((β_v / β_s) - 1)

Označme r_e vzdálenost Země-Slunce a r_v vzdálenost Venuše-Slunce. Nyní můžeme vyjádřit paralaxu Venuše jako β_v = AB / (r_e- r_v) a paralaxu Slunce β_s = AB / r_e, kde podíl β_v / β_s = r_e / (r_e- r_v). Dosazením do rovnice pro Δβ dostaneme

Δβ = β_s ((r_e / (r_e- r_v)) - 1) = β_s r_v / (r_e- r_v)

Speciálně pak můžeme vyjádřit sluneční paralaxu

β_s = Δβ ((r_e / r_v) - 1)

Zdůrazněme, že Δβ je úhlová vzdálenost, tedy úhlová vzdálenost mezi úsečkami.

Podíl r_v / r_e můžeme vyjádřit pomocí třetího Keplerova zákona, neboť známe dobu oběhu Venuše (224,7 dní) a Země (365,25 dní).

(r_e / r_v)³ = (365,25 / 224.7)²

z toho

r_e / r_v = 1,38248

Dosazením tohoto vztahu do vztahu pro paralaxu dostaneme

β_s = Δβ ((r_e / r_v) - 1) = Δβ (1,38248 - 1)

z toho

&beta_s = 0,38248 Δβ

Konečně dle definice paralaxy je vzdálenost Země od Slunce r_e

r_e = AB / β_s

Takže pro výpočet astronomické jednotky je třeba určit vzdálenost AB mezi dvěma pozorovateli a úhlovou vzdálenost &Deltaβ z pozorovacích dat přechodu Venuše před Sluncem.

Pozorování z roku 1769

Níže jsou uvedeny časy kontaktů pozorovaných v různých místech. Kresba umístěná níže byla publikována v knize A. Pannekoek: „A History of Astronomy“ a uvádí přechody v letech 1761 a 1769.

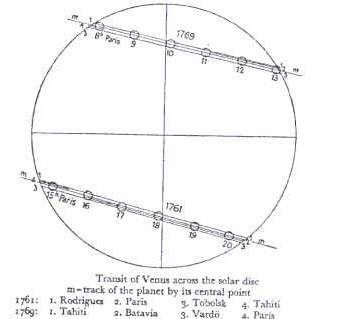
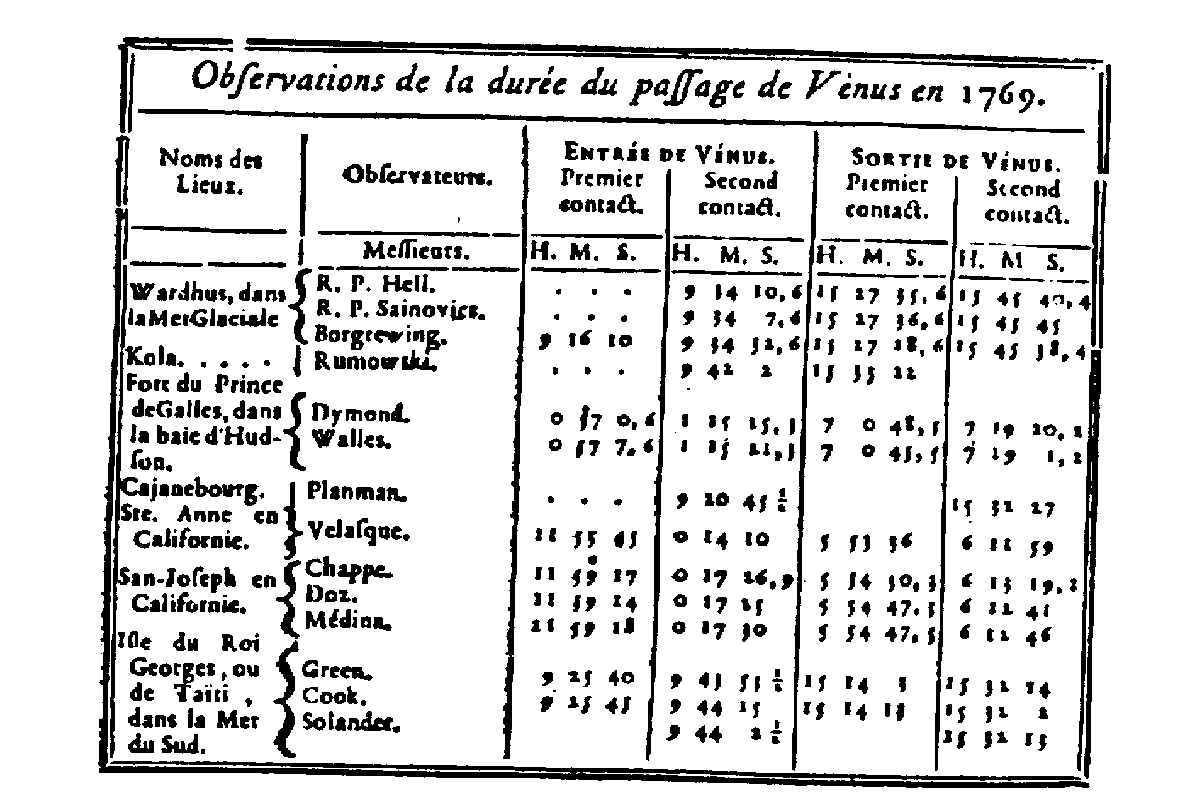
K výpočtu využijeme přechody z roku 1769 pořízené ve Vardö (přímka 3) a na Tahiti (přímka 1).

1) Vzdálenost pozorovatelů v místech A a B na Zemi

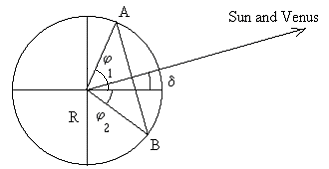
Vzdálenost AB může být určena ze znalosti zeměpisných šířek pozorovacích míst A a B. Na obrázku jsou φ₁ a φ₂ zeměpisné šířky míst A a B a R je poloměr Země.

V pravoúhlém trojúhelníku, který je polovinou rovnoramenného trojúhelníku RAB platí

sin ((φ₁ + φ₂) / 2) = (AB / 2) / R

Pak vzdálenost AB je

AB = 2 R sin ((φ₁ + φ₂) / 2)

Uvědomte si: leží-li obě města na stejné polokouli je úhel roven (φ₁ - φ₂) / 2 a navíc geometrická situace se změní, když mají města různé zeměpisné délky.

Vardö (Laponsko) a Papeete (Tahiti) mají stejnou zeměpisnou délku (poledník) a jejich zeměpisné šířky jsou 70° 21' N a 17° 32' S. Dodejme, že ve ve Vardö byl polární den.

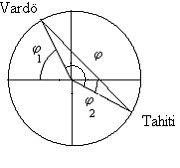
V tomto případě se mění geometrická situace a je třeba uvažovat nový úhel φ

φ = (90 - φ₁) + 90 + φ₂ = 127° 11'

a dosazením poloměru Země R = 6378 km můžeme vypočítat vzdálenost míst

AB = 2 R sin(φ / 2) = 11425 km

2) Vzdálenost Δβ dvou pozorovaných stop Venuše?

Abychom vypočítali úhlovou vzdálenost δβ, změříme délkový průměr Slunce D a délkovou vzdálenost A'B' mezi dvěma stopami na nákresu nebo fotografii. Úhlový průměr Slunce pozorovaného ze Země je 30' (úhlových minut, t.j. 30 / 60°). Pomocí jednoduché úměry dostáváme

Δβ/30' = A'B' / D

z toho

Δβ = (30') (A'B' / D),

ale do vztahu je nutno dosadit úhlový průměr Slunce v radiánech. Tedy

Δβ = (30 π / 10800) (A'B'/ D),

Δβ= (π /360) (A'B' / D)

Přímým měřením vzdáleností úseček 1 a 3 dostaneme Δβ = 1,5 mm a průměr Slunce D = 70 mm. Odtud

Δβ = (π / 360)(1,5 / 70) = 0,0019 radiánů

Přímé měření úhlové vzdálenosti Δβ by bylo zatíženo větší chybou, neboť měření úhlové vzdálenosti dvou rovnoběžek je obecně obtížnější. Pro dosažení přesnější hodnoty Δβ mohou studenti využít přesnější metodu s využitím Pythagorovy věty.

Použitím vztahu pro paralaxu máme

β_s = 0,38248 Δβ

a užitím vztahu pro sluneční paralaxu je vzdálenost Země od Slunce r_e

r_e = AB / β_s

S využitím dat pořízených expedicemi v roce 1769 můžeme vypočítat hodnotu r_e

r_e = 157 10⁶ km

V současnosti udávaná vzdálenost Země-Slunce je r_e = 149,6 10⁶ km. Provedeme-li mnohem přesnější měření Δβ můžeme dosáhnout přesnější hodnoty astronomické jednotky.

Třetí Keplerův zákon

Třetí Keplerův zákon říká, že polosy a_v, a_e eliptických drah Venuše a Země jsou svázány s dobami jejich oběhu T_v, T_e následujícím vztahem:

(a_e / a_v)³ = (T_e / T_v)²

Budeme-li pro zjednodušení předpokládat,že se Venuše a Země pohybují po kruhových drahách, je možno polosy nahradit poloměry r_v a r_e a tak dostáváme vztah

(r_e / r_v)³ = (T_e / T_v)²

Sluneční paralaxa (horizontální paralaxa)

Podle definice je paralaxa Slunce úhel β (viz níže)

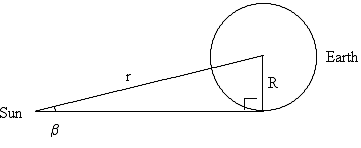
Na základě trigonometrie je sin β = R / r, ale protože je úhel β velmi malý, může být nahrazen přímo hodnotou β měřenou v radiánech. R je poloměr Země a r je vzdálenost Země-Slunce. Pak můžeme určit r podle vztahu

r = R / β

Výpočet Δβ měřením sečen

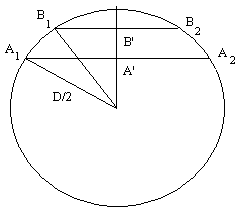
Vzdálenost Δβ mezi sečnami A a B je velmi obtížné měřit, neboť jejich vzdálenost je ve srovnání s průměrem Slunce velmi malá. Měření úsečky A'B' je vhodnější nahradit měřením sečen A₁A₂ a B₁B₂, trajektorií Venuše nma slunečním disku pořízených dvěma pozorovateli A a B.

S využitím Pythagorovy věty dostaneme

B'S = ((D² - B₁B₂²)/2)^1/2

A'S = ((D² - A₁A₂²)/2)^1/2

K určení A'B' potřebujeme vypočítat rozdíl B'S - A'S

A'B' = [(D² - B₁B₂²)^1/2 - (D² - A₁A₂²)^1/2]/2

Podělením průměrem D dostaneme

A'B' / D = [(1 - (B₁B₂ / D)²)^1/2 - (1 - (A₁A₂ / D)²)^1/2]/2

Měřením A1A2, B1B2 a D v historickém obrázku přechodu Venuše dostaneme A₁A₂ = 52 mm (stopa 3), B₁B₂ = 49 mm (stopa 1) a D = 70 mm. Pak

A'B' / D = [(1 - (49 / 70)²)^1/2 - (1 - (52 / 70)²)^1/2]/2 = 0.02235

a Δβ je

Δβ = (31 π /360) 0.02235 = 0,00020 radiánů

Užitím vztahu pro paralaxu máme

β_s = 0.38248 Δβ

a užitím vztahu pro solární paralaxu dostaneme vzdálenost r_e Země - Slunce

r_e = AB / β_s

S využitím dat expedic z roku 1769 a AB = 11425 km můžeme vypočítat

r_e = 149 10⁶ km

Jak si můžete povšimnout, je obtížné dostat rozumný výsledek, ačkoliv tento výsledek je docela blízko v současnosti přijímané hodnotě.

Venus Transit 2004