G4 - Vzdálenosti ve sluneční soustavě: paralaxy a Keplerovy zákony
Zde si můžete stáhnout tento dokument v PDF [132kB].
Astronomové při sledování oblohy zaznamenávají především úhly a pozorují něco, co se nazývá „nebeská sféra“. Nicméně, hvězdy nejsou od Země vždy ve stejné vzdálenosti. Jak tedy můžeme měřit velikost Země, vzdálenost hvězd, planet či rozumět neustálému pohybu ve vesmíru?
Abychom tomu mohli rozumět, je nezbytnou součástí rozumět pojetí paralax.
Pokud dva různí pozorovatelé sledují stejný objekt pod různými úhly, znamená to, že onen objekt není nekonečný. Rozdíl v úhlech závisí pouze na poloze pozorovatelů a vzdálenosti objektu. Tak vzniká obrysový jev, který vytváří náš mozek spolu s různými obrazy přicházejícími z našich očí. Čím je vzdálenost větší, tím více nezávislých pozorovatelů potřebujeme. Tento jev využíváme k měření vzdálenosti nebeských objektů, kterou nemůžeme změřit přímo. Na Zemi se používá této metody k měření vzdálených míst, aniž bychom museli ona místa navštívit. Metodu nazýváme triangulací.
Triangulace
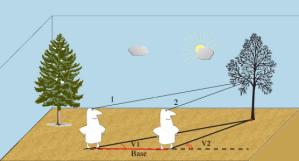
Začněme měřením vzdálených objektů na Zemi. Tímto způsobem můžeme postupně mapovat zemský povrch. Použijeme triangulaci: díváme se na objekt z místa 1 a vidíme ho pod daným úhlem V1, poté se posuneme o známou vzdálenost zvanou „základna“ do místa 2, odkud vidíme objekt pod úhlem V2. Známe dva úhly a jednu vzdálenost, čímž pro nás není problém spočítat vzdálenost objektu ze znalosti trojúhelníkové geometrie. V astronomii se tento úkon nazývá paralaxa.
pojem paralaxy
Paralaxa v astronomi
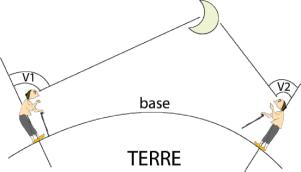
Pokud chceme v astronomii spočítat vzdálenost nebeského tělesa od Země, můžeme použít podobný postup, jako je triangulace. Daný nebeský objekt pozorujeme ze dvou různých míst na Zemi, a jelikož známe vzdálenost oněch míst – základnu, snadno spočítáme jeho vzdálenost. Je jasné, že tato metoda má svůj limit, kterým je vzdálenost pozorovatelen. Zemský průměr je 12 756 km a tato vzdálenost nemůže být samozřejmě překročena. Pokud jsou tedy hvězdy příliš vzdálené od Země, tato metoda se stává neefektivní.
Počítání vzdáleností pomocí paralaxy
Příklad: počítání vzdáleností pomocí triangulace
Měření vzdáleností pomocí triangulace
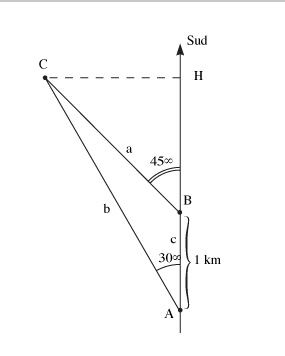
Chceme změřit vzdálenost CH mezi budovou C a cestou ABH ležící podél směru sever-jih, kterým pozorovatel cestuje. Ten může měřit úhly či vzdálenosti pouze z cesty ABH. V pozici A zaznamenal úhel 300 mezi cestou a jižním směrem. Z pozice B, vzdálené od pozice A 1 km, zaznamenal pozorovatel úhel 450. K vypočítání vzdálenosti CH použijeme trojúhelník ABC, známe dva úhly a základnu AB.
a/sin(A) = B/sin(B) = C/sin(C), kde (A), (B), (C) jsou úhly A, B, C trojúhelníku ABC.
Takže dostáváme: a/sin(30°) = 1 km/sin(C) kde (C) = 180° - ((A)+(B)) = 180° -165° = 15°, a proto a = sin(30°)/sin(15°. Ale CH = a.sin(B) = sin(45°), a proto CH = 1366 m
Denní paralaxa a horizontální paralaxa
Ukázali jsem si, že triangulace a paralaxa využívají k měření vzdáleností dalekých objektů podobných principů. Je důležité zmínit, že přesnost měření závisí na délce základny. Je též důležité, abychom byli schopni měřit úhly s dostatečnou přesností. Pro nebeské těleso nepříliš vzdálené od Země je dostatčující, pokud změříme úhly na dvou odlišných místech na zemském povrchu ve stejnou dobu.
Je známo, že během otáčení Země kolem své osy dochází i k pohybu pozorovatelů. To zapříčiňuje změnu úhlu, pod kterým nebeské těleso o konečné vzdálenosti pozorujeme, v porovnání s úhlem od středu Země. Tento jev je nazýván „denní paralaxa“, která se na daném místě na zemském povrchu během dne mění.
Vzdálenost, která odděluje dva pozorovatele, může sloužit jako „základna“. Je na první pohled jasné, že maximální základnou je zemský průměr.
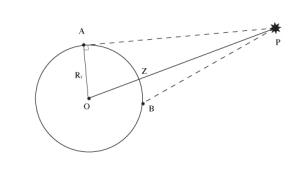
Denní paralaxa má své maximum. To se nazývá horizontální paralaxa, což je úhlová velikost zemského poloměru viděná z pozorovaného objektu.
Roční paralaxa
Protože jsou hvězdy velmi vzdálené, základna o rozměrech zemského průměru je příliš malá na to, abychom ji mohli využít při triangulaci. Proto se nabízí řešení použitím tzv. roční paralaxy, což je úhlová velikost zemského poloměru viděná z hvězdy. My vlastně pozorujeme zdánlivý směr hvězdy z různých pozic oběžné dráhy Země, jak putuje kolem Slunce. Průměr orbity (cca 300 000 000 km) je značně větší základnou, než v již zmíněném případě. Pokud má roční paralaxa velikost jedné úhlové vteřiny, pak říkáme, že hvězda je vzdálena od Země jeden parsek. Avšak pouze málo hvězd má měřitelnou paralaxu ze Země. Astrometrické satelity (Hipparchos v minulosti a Gaya v budoucnu) proto velice pomáhají při získávání údajů o hvězdách, jejichž „měřitelnost“ je ze Země neproveditelná.
Měření vzdáleností hvězd pomocí roční paralaxy vzhledem k pohybu Země kolem Slunce
Toto měření je v postatě stejné jako triangulace či paralaxa, avšak probíhá v šesti měsíčních intervalech. Měření paralaxy je přesné pro měření blízkých hvězd, avšak se vzrůstající vzdáleností se jeho přesnost zmenšuje. Vzdálenost nejvzdálenějších hvězd se provádí pomocí statistik, spektroskopie a fotometrie.
Paralaxa a vzdálenost Slunce–Země
Ukázali jsme si, jak astronomové měří vzdálenost hvězd a planet. Jak však mohou měřit vzdálenosti v celé sluneční soustavě? Jak můžeme z pozorování přechodu Venuše přesně změřit vzdálenost Země–Venuše?
Abychom tomu všemu rozuměli, podívejme se nejprve na to, jak změřit paralaxu planety. Naznačili jsme, že je nutné provést měření úhlu pohledu na nebeské těleso a porovnat ho s pevně daným směrem, pro oba pozorovatele známým. Tento daný směr může představovat nějaká hvězda, která se na obloze vyskytuje v blízkosti pozorované planety, avšak od Země dostatečně vzdálená na to, aby mohla být považovaná za nekonečně vzdálenou. Jinými slovy se dá říci, že paralaxa oné hvězdy je rovna nule: kdybychom ji pozorovali ze všech míst na Zemi, její směr by se nezměnil – byl by stále stejný. Tudíž lze použít hvězdu, jejíž denní paralaxa je zanedbatelná. Taková metoda byla poprvé využita na planetu Mars již v 17. století, avšak měření směru hvězdy bylo příliš obtížné. Z toho důvodu se hledalo nějaké jednodušší řešení. Planeta Venuše, přecházející rovnoměrně přes sluneční disk, přinesla řešení. V době, jakou je napříkladpřechod, slouží sluneční disk jako vztažná jednotka, proti níž se Venuše jeví z různých míst různě. Záleží na principu paralaxy.
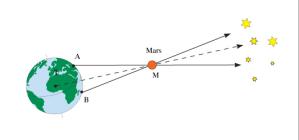
Případ Marsu: Planeta se ukazuje před různými hvězdami v závislosti na umístění pozorovatele
Vzdálenost Země–Mars můžeme vypočítat jen na základě principu paralaxy a znalosti základny.
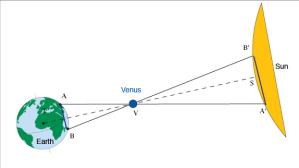
Případ Venuše: Projekce tmavého planetárního disku na sluneční kotouč v čase přechodu se liší pro dva pozemské pozorovatele.
V případě Venuše je Slunce využito (jak jsme se již zmínili) jako vztažná jednotka při počítání paralaxy. Nicméně je zde jeden podstatný rozdíl od případu s Marsem. Slunce je v konečné vzdálenosti a samo má paralaxu. Proto musíme znát poměr vzdáleností Venuše–Slunce a Země–Slunce. Tato znalost je zajištěna znalostí Keplerových zákonů. Známe vzdálenost AB, úhel V (od pozorovatelů), a poměr VA/VA´ (Kellerův třetí zákon). Poté odvodíme VT, VS a TS; vzdálenost Země–Slunce je 1AU. Problém se však komplikuje vzhledem k faktu, že A a B se pohybují spolu se zemskou osou a také T a V se pohybují v důsledku toho, že se Země i Venuše pohybují po oběžné dráze kolem Slunce.
Vzdálenosti v sluneční soustavě a třetí Keplerův zákon
Princip paralaxy nedostačuje k tomu, aby se mohly určit všechny vzdálenosti ve sluneční soustavě. Pouze planety Mars a Venuše, případně asteroidy jako např. Eros, které se pohybují blízko Země, jsou pro nás přímo „měřitelné“. Slunce a ostatní planety jsou příliš vzdálené, avšak díky znalosti Keplerových zákonů můžeme takové problémy snadno vyřešit.
První Keplerův zákon tvrdí, že oběžné dráhy planet jsou elipsy. Tento zákon potřebujeme použít, jelikož se vzdálenosti Země–Venuše a Země–Slunce mění s časem, v němž se tato tělesa po svých oběžných drahách pohybují.
Keplerův druhý zákon hovoří o konstantních plochách a dá se z něho jednoduše odvodit to, že se planety pohybují tím rychleji, čím jsou ke Slunci blíže. Při analýze pozorování přechodu Venuše to je pro nás velice vhodný poznatek, pro jehož aplikaci musíme znát zdánlivou rychlost pohybu Venuše přes solární disk.
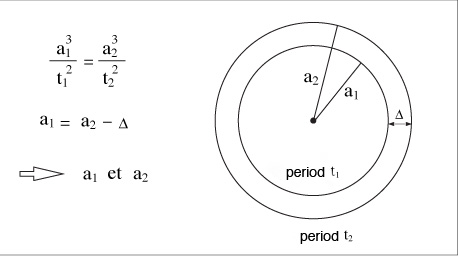
Třetí Keplerův zákon nám ukazuje souvislosti se vzdáleností Slunce od všech planet naší soustavy. Budeme-li znát pouze jednu takovou vzdálenost, pak pro nás není velký problém spočítat všechny ostatní vzdálenosti. Je dáno, že platí následující vztah: A3/T2 je konstantní pro všechny planety. A je hlavní poloosa orbity a T je čas oběhu kolem Slunce. Obrázek jasně ukazuje, co nastává v případě, kdy považujeme oběžné dráhy za kruhové. Známe vzdálenost Δ a doby oběhů t1 a t2.
Keplerův třetí zákon
První Keplerův zákon tvrdí, že oběžné dráhy planet jsou elipsy. Proto není možné říci, že vzdálenosti Země–Slunce a Slunce–Venuše jsou stejné jako délka hlavní poloosy oběžné dráhy Země–Slunce a Venuše–Slunce. Známe-li délku hlavní poloosy a, pak můžeme podle vztahu:
rP = a (1 - e cos E)
vypočítat polohový vektor (průvodič) rp. E značí excentrickou anomálii (poloha planety na své oběžné dráze) a e je excentricita elipsy (oběžné dráhy).
Závěr
Princip paralaxy a Keplerovy zákony jsou skutečné dostačující nástroje ke zjištění vzdálenosti Země–Venuše a navíc také ke zjištění všech ostatních vzdáleností ve sluneční soustavě. A když bude vzdálenost Slunce–Země naší „základnou“ pro měření vzdáleností blízkých hvězd, pak již můžeme měřit celý vesmír.