Úvod Fotogalerie Výpočet AU Historie O škole English version

Výpočet AU

Výpočty zjednodušíme a budeme počítat s kruhovou oběžnou drahou Země i Venuše a předpokládat, že se pozoruje ze dvou míst na stejném poledníku.

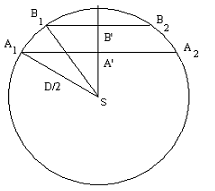
Dvěma pozorovatelům na různých místech se Venuše promítne vzhledem ke Slunci jinde. Tato situace je zakreslena na prvním obrázku. Body A‘ a B‘ symbolizují místa, kde vidí Venuši pozorovatel z bodu A a z bodu B. Bod S je střed slunce.

Na následujícím obrázku je vidět situace z bočního pohledu. Z-střed Země, S-střed slunce, r_e-vzdálenost středů Země-Slunce, r_v-vzdálenost středů Venuše-Slunce.

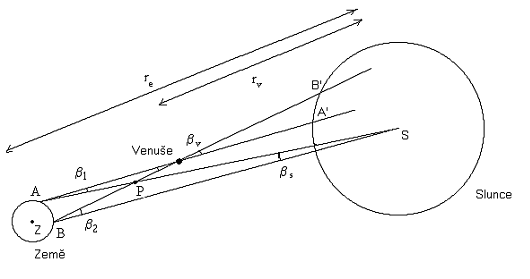
Ze shodnosti úhlů APV a BPS vyplývá:

Δβ = β_s ((β_v / β_s) - 1)

Nyní můžeme vyjádřit paralaxu Venuše jako β_v = |AB| / (r_e - r_v) a paralaxu Slunce β_s = |AB| / r_e.

Podíl β_v / β_s = r_e / (r_e - r_v). Dosazením do rovnice pro Δβ dostaneme:

Δβ = β_s r_v / (r_e - r_v)

Z toho vypočítáme β_s:

β_s = Δβ ((r_e / r_v) – 1)

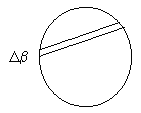
Zdůrazněme, že Δβ je úhlová vzdálenost, tedy úhlová vzdálenost mezi úsečkami.

Podíl r_v / r_e můžeme vyjádřit pomocí třetího Keplerova zákona, neboť známe dobu oběhu Venuše a Země. Platí třetí Keplerův zákon: a₁³/ t₁² = a₂³/ t₂²

Z toho si odvodíme vzorec: a₁³ / a₂³ = t₁² / t₂²

a₁ odpovídá v našem případě úsečce r_e
a₂ odpovídá v našem případě úsečce r_v

Oběžná doba Země je t₁ = 365,25 dní a oběžná doba Venuše je t₂ = 224,7 dní.

Naposledy upravíme tento vzorec do podoby:

(r_e / r_v)³ = (t₁ / t₂)²
(r_e / r_v)³ = (365,25 / 224,7)²
r_e / r_v = 1,38248

Dosazením do vztahu pro paralaxu dostaneme:

β_s = Δβ ((r_e / r_v) - 1) = Δβ (1,38248 - 1)
ß_s = 0,38248 Δβ

Konečně dle definice paralaxy je vzdálenost Země od Slunce r_e

r_e = |AB| / β_s
r_e = |AB| / 0,38248 Δβ

Nyní už stačí určit pouze vzdálenost |AB| a Δβ z pozorovacích dat.

Vzdálenost |AB| může být určena ze znalosti zeměpisných šířek pozorovacích míst A a B. φ1 a φ2 jsou zeměpisné šířky míst A a B a R je poloměr Země:

|AB| = 2*R*sin((φ₁ + φ₂) / 2)

Uvědomme si, že leží-li obě místa na stejné polokouli je úhel roven (φ1 - φ2) / 2.

Následuje výpočet Δβ měřením sečen (viz první obrázek):

Vzhledem k tomu, že vzdálenost Δβ mezi sečnami A a B je v porovnání s průměrem Slunce velmi malá, je obtížné ji měřit. Měření úsečky |A'B'| nahradíme měřením sečen |A₁A₂| a |B₁B₂|, trajektorií Venuše na slunečním disku pořízených dvěma pozorovateli A a B.

S využitím Pythagorovy věty dostaneme:

|B'S| = ((D² - |B₁B₂|²)/4)^1/2
|A'S| = ((D² - |A₁A₂|²)/4)^1/2

K určení |A'B'| potřebujeme vypočítat rozdíl |B'S| - |A'S|

|A'B'| = [(D² - |B₁B₂|²)^1/2 - (D² - |A₁A₂|²)^1/2]/2

Dělením průměrem D dostaneme:

|A'B'| / D = [(1 - (|B₁B₂| / D)²)^1/2 - (1 - (|A₁A₂| / D)2)^1/2]/2

Úhlový průměr Slunce pozorovaného ze Země si označíme jako U(ve stupních). Pomocí jednoduché úměry dostáváme:

Δβ/U = |A'B'| / D

z toho vyplývá, že:

Δβ = U(|A'B'| / D),

ale do vztahu je nutno dosadit úhlový průměr Slunce v radiánech. Tedy:

ΔΒ = (U π / 180) (|A'B'| / D),

A užitím vztahu pro solární paralaxu dostaneme vzdálenost r_e Země - Slunce:

r_e = |AB| / 0.38248 (U π / 180) (|A'B'| / D)

Sportovní Gymnázium a Gymnázium Kladno