Home Photogalery AU calculation History About school Česká verze

Calculation of AU

We will count with circular Earth and Venus track. We expect observers are on two places at the same meridian.

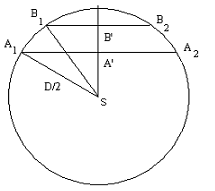
Venus will project onto Sun disc on different places for each observers. This situation is drawn in first picture. Points A' and B' symbolise places where observer can see Venus from point A and B. Point S is middle of the Sun.

In next picture, there is Sun from side view. Z-middle of the Earth, S-middle of the Sun, r_e - distance of middles Earth-Sun, r_v - distance of middles Venus-Sun

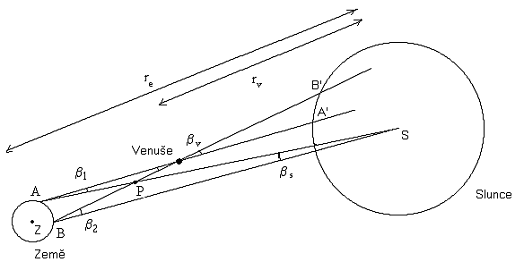
Congruence of angles APV and BPS says:

Δβ = β_s ((β_v / β_s) - 1)

Now we can get value of Venus parallax with β_v = |AB| / (r_e - r_v) and Sun Parallax β_s = |AB| / r_e.

Quotient β_v / β_s = r_e / (r_e - r_v). When we place it to equation for Δβ we will get:

Δβ = β_s r_v / (r_e - r_v)

We can count β_s:

β_s = Δβ ((r_e / r_v) – 1)

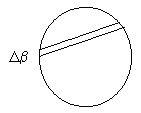
We will define Δβ as angle distance between segments of lines.

We can get r_v / r_e from Third Kepler Law, because we know the time of Venus and Earth orbit. There stand Third Kepler Law: a₁³/ t₁² = a₂³/ t₂²

We elicit of it a formula: a₁³ / a₂³ = t₁² / t₂²

a₁ matches to segment of line r_e
a₂ matches to segment of line r_v

Time of Earth orbit is t₁ = 365,25 days and time of Venus orbit is t₂ = 224,7 days.

At last, we modify this formula to:

(r_e / r_v)³ = (t₁ / t₂)²
(r_e / r_v)³ = (365,25 / 224,7)²
r_e / r_v = 1,38248

If we substitute this to formula for parallax, we will get:

β_s = Δβ ((r_e / r_v) - 1) = Δβ (1,38248 - 1)
ß_s = 0,38248 Δβ

Finally, according to parallax definition, the distance Earth-Sun r_e

r_e = |AB| / β_s
r_e = |AB| / 0,38248 Δβ

Now, we can calculate |AB| and Δβ from observed data.

Distance |AB| can be obtained with knowledge of observation places latitudes A and B. φ1 and φ2 are Earth latitudes of places A and B and R is an Earth diameter:

|AB| = 2*R*sin((φ₁ + φ₂) / 2)

If both places lay on the same hemisphere, an angle matches (φ1 - φ2) / 2.

Calculation of Δβ from bisectors (first picture):

According to little value of distance Δβ between bisectors A and B it is difficult measure it. We replace caculation of line segment |A'B'| by calculation of bisectors |A₁A₂| a |B₁B₂| (trajectories of Venus on Sun disc obtained by observers from A and B).

If we use Pythagorean theorem, we will get:

|B'S| = ((D² - |B₁B₂|²)/4)^1/2
|A'S| = ((D² - |A₁A₂|²)/4)^1/2

We need to count difference |B'S| - |A'S| to set |A'B'|

|A'B'| = [(D² - |B₁B₂|²)^1/2 - (D² - |A₁A₂|²)^1/2]/2

When we divide by diameter, we get:

|A'B'| / D = [(1 - (|B₁B₂| / D)²)^1/2 - (1 - (|A₁A₂| / D)2)^1/2]/2

Sun angle diameter which is observed from Earth, we point as U (in degrees). With the help of simple rule of proportion we get:

Δβ/U = |A'B'| / D

It says:

Δβ = U(|A'B'| / D),

Now, we have to substite Sun angle diameter in radians. Now we get

ΔΒ = (U π / 180) (|A'B'| / D),

If we use a formula for solar parallax, we will get a distance r_e Earth-Sun:

r_e = |AB| / 0.38248 (U π / 180) (|A'B'| / D)

Sports Secondary Grammar School and Grammar School Kladno